Thinking in Data Structure -- AVL Tree

AVL 树， 是在二叉搜索树的基础上，在插入操作上加入了旋转的操作，从而避免了一棵树退化成一个链表或者树的深度过长导致搜索的时候效率太低的坏处，而旋转也是 AVL 树 中最重要的操作，也是本博文的重点内容。

AVL 树 在普通二叉搜索树节点的基础上加入了一个 buf 值，意思是左孩子的高度减去右孩子的高度，而 buf 值的合法范围是 -1， 0， 1，如果不是这几个值，那么说明树不平衡，就要进行旋转。

接下来我们重点说说旋转操作。

首先，要注意的是，在实现中并不是等到节点的 bf 值变为 +2 或者 -2 的时候才进行旋转。相反，当父节点的 bf 为 +1 或者 -1 时，就认为下一次插入的是必将导致不平衡，所以就进行旋转了。

以左失衡为例，分为 LL 和 LR，即在父节点的左子树的左节点插入或者是父节点的左子树的右节点插入。究竟在插入的时候是如何判断这两种情况的，我们来看一张图

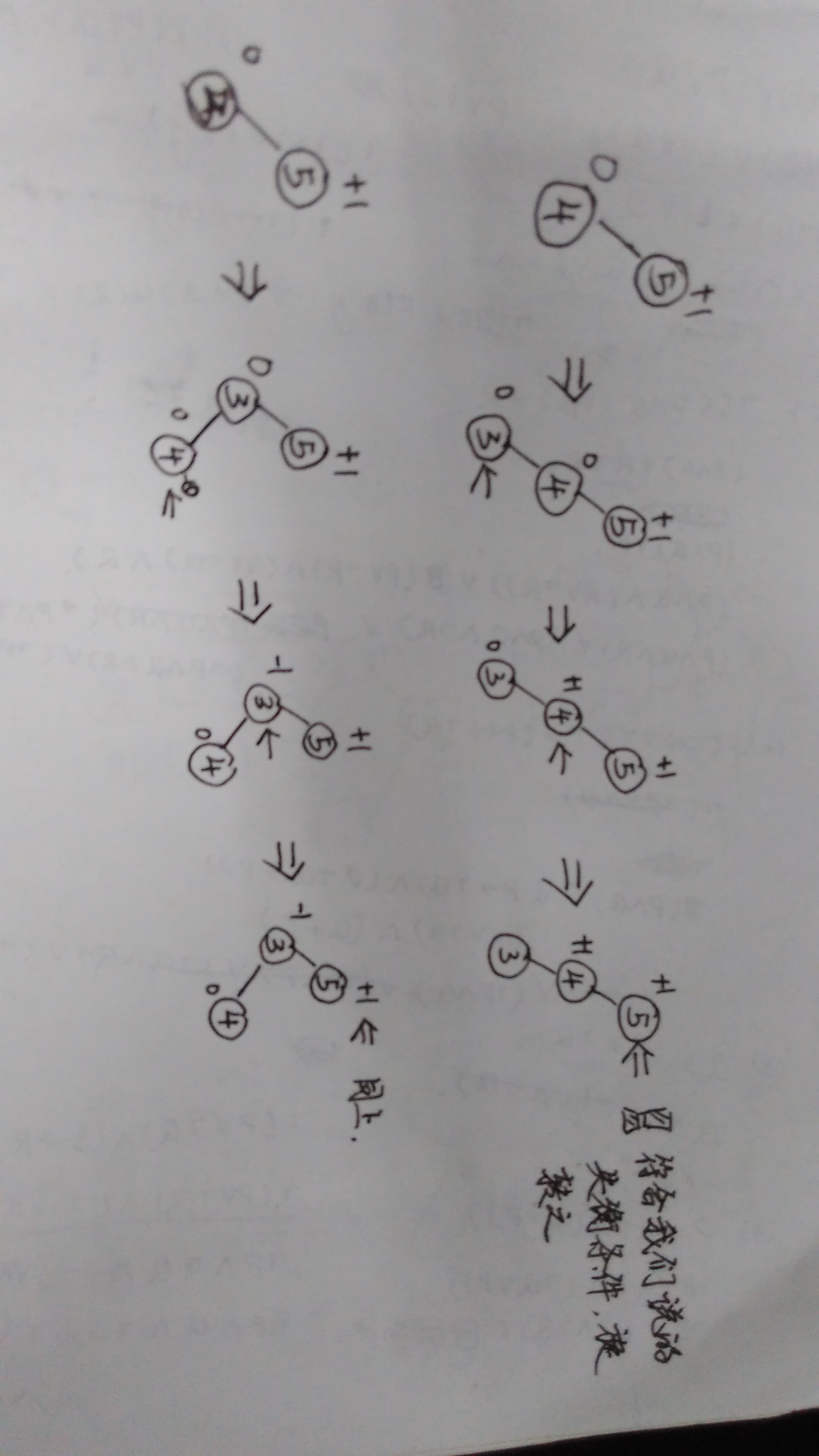
从图中我们可以看到，当父节点的左儿子的 bf 是 +1 时，属于 LL 的情况， -1 的时候，属于 LR 的情况。那么继续分析下去， bf 等于 0 的时候是属于那种情况？稍加思考便可发现，这一种情况不存在，因为我们这里讨论的父节点的左儿子的 bf 值是在插入新节点之后导致失衡的前提下，如果左节点的左儿子在插入新节点之后导致失衡而且 bf 为 0，也就是在插入新节点之前以及之后父节点的左子树的高度没有发生变化，那么在插入新节点之后树发生了失衡，那么说明在插入之前树也是失衡的。

有了上面的思考，接下来我们来分析一下旋转之后各节点的 bf 值如何调整，LL 的比较简单，重点来看 LR 的，还是来看一个图：

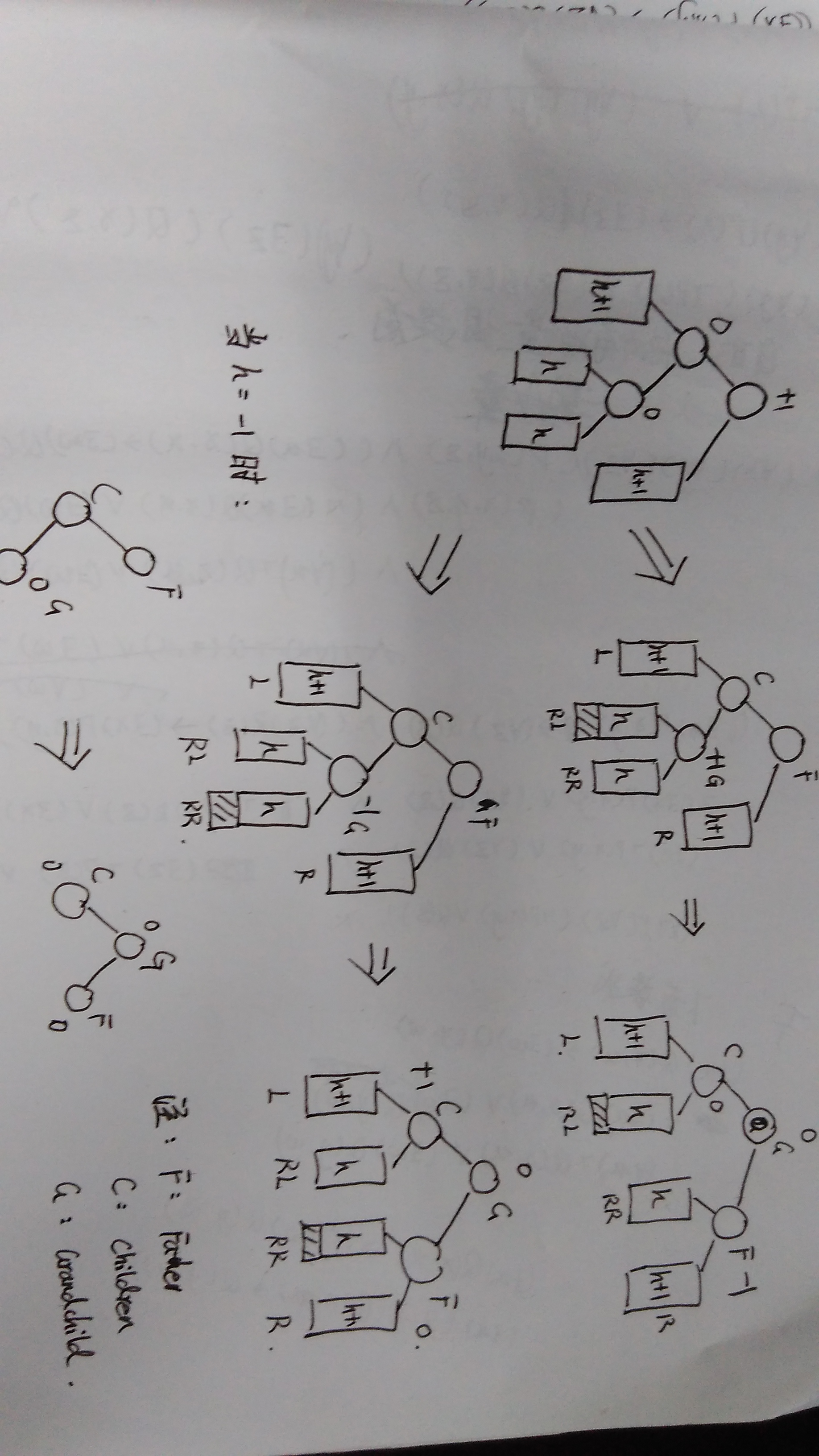
从图中我们可以看到，LR 分为三种情况，这三种情况分别是通过父节点左子树的右节点或者说是 “孙子节点” 插入后的 bf 值来区分的。

而右失衡的操作，跟左失衡类似，在这里就不再赘述了。

下面是代码的实现：

#include "avl.h"
#include <stdlib.h>

void insert(p_avl *t, int data)
{
	if (*t != NULL) {
		if (data < (*t)->data) {
			insert(&(*t)->l_child, data);
			if (unblance) {
				switch ((*t)->buf) {
				case 0:
					(*t)->buf = 1;
					break;
				case -1:
					(*t)->buf = 0;
					unblance = false;
					break;
				case 1:
					left_rotation(t);
					break;
				}
			}
		} else if (data > (*t)->data) {
			insert(&(*t)->r_child, data);
			if (unblance) {
				switch ((*t)->buf) {
				case 0:
					(*t)->buf = -1;
					break;
				case 1:
					(*t)->buf = 0;
					unblance = false;
					break;
				case -1:
					right_rotation(t);
					break;
				}
			}
		} else {
			unblance = false;
			fprintf(stderr, "The key has already in the tree");
		}
	} else {
		unblance = true;
		
		*t = (p_avl)malloc(sizeof(avl));
		if (*t == NULL) {
			fprintf(stderr, "Out of memory!\n");
			exit(1);
		}
		(*t)->data = data;
		(*t)->buf = 0;
		(*t)->l_child = (*t)->r_child = NULL;
	}
}

void right_rotation(p_avl *parent)
{
	p_avl child;

	child = (*parent)->r_child;
	if (child->buf == -1) {
		p_avl child_left;

		child_left = child->l_child;
		(*parent)->r_child = child_left;
		child->l_child = (*parent);
		(*parent)->buf = 0;
		(*parent) = child;
	} else {
		p_avl grandchild = child->l_child;
		p_avl grandchild_right = grandchild->r_child;
		
		child->l_child = grandchild_right;
		grandchild->r_child = child;
		(*parent)->r_child = grandchild->l_child;
		grandchild->l_child = (*parent);

		switch (grandchild->buf) {
		case 0:
			(*parent)->buf = child->buf = 0;
			break;
		case 1:
			(*parent)->buf = 0;
			child->buf = -1;
			break;
		case -1:
			(*parent)->buf = 1;
			child->buf = 0;
			break;
		}
		(*parent) = grandchild;
	}
	(*parent)->buf = 0;
}

void left_rotation(p_avl *parent)
{
	p_avl child;

	child = (*parent)->l_child;
	if (child->buf == 1) {
		p_avl child_right;

		child_right = child->r_child;
		(*parent)->l_child = child_right;
		child->r_child = (*parent);
		(*parent)->buf = 0;
		(*parent) = child;
	} else {
		p_avl grandchild = child->r_child;
		p_avl grandchild_left = grandchild->l_child;

		child->r_child = grandchild_left;
		grandchild->l_child = child;
		(*parent)->l_child = grandchild->r_child;
		grandchild->r_child = (*parent);

		switch (grandchild->buf) {
		case 0:
			child->buf = (*parent)->buf = 0;
			break;
		case 1:
			child->buf = 0;
			(*parent)->buf = -1;
			break;
		case -1:
			child->buf = 1;
			(*parent)->buf = 0;
			break;
		}
		(*parent) = grandchild;
	}
	(*parent)->buf = 0;
}

void pre_order(p_avl t)
{
	if (t) {
		printf("%d ", t->data);
		pre_order(t->l_child);
		pre_order(t->r_child);
	}
}

int main(void)
{
	p_avl root = NULL;
	int key;

	while ((scanf("%d", &key)) && key != '#') {
		insert(&root, key);
	}
	pre_order(root);
}